Skip to main content

Formation avancée: Outils de développement et de performance

Chapitre 3 Mesurer et comparer des temps d’exécution

La première étape avant d’optimiser un code est de pouvoir mesurer son temps d’exécution, afin de pouvoir comparer les temps d’exécution entre différente implémentations.

Pour plus de détails à propos du contenu de ce chapitre ainsi que du suivant, nous renvoyons au livre d’Hadley Wickham Advanced R 4, librement accessible en ligne.

3.1 Mesurer des temps d’exécution avec system.time()

Pour mesurer le temps d’exécution d’une commande , on peut utiliser la fonction system.time() comme ceci :

obs <- matrix(rep(1.96, 2), nrow=2, ncol=1)
system.time(mvnpdf(x=obs, Log=FALSE))
##    user  system elapsed 
##   0.001   0.000   0.004

Le problème qui apparaît sur cet exemple est que l’exécution est tellement rapide que system.time() affiche 0 (ou une valeur très proche). De plus, on voit qu’il y a une certaine variabilité quand on relance plusieurs fois la commande. Ceci rend la comparaison avec une autre implémentation (que l’on espère) plus rapide pour le moins délicate.

Ainsi si on souhaite comparer notre code avec la fonction mvtnorm::dmvnorm(), on ne peut pas utiliser system.time() :

system.time(mvtnorm::dmvnorm(rep(1.96, 2)))
##    user  system elapsed 
##   0.003   0.002   0.008

On pourrait se dire qu’il faut augmenter la complexité de notre calcul, mais il y a mieux : utiliser le package microbenchmark !

3.2 Comparer des temps d’exécution avec microbenchmark()

Comme son nom l’indique, ce package permet justement de comparer des temps d’exécution même quand ceux-ci sont très faibles. De plus, la fonction microbenchmark() va répéter un certain nombre de fois l’exécution des commandes, ce qui va stabiliser son résultat.

library(microbenchmark)
mb <- microbenchmark(mvtnorm::dmvnorm(rep(1.96, 2)),
                     mvnpdf(x=matrix(rep(1.96,2)), Log=FALSE),
                     times=1000L)
## Warning in microbenchmark(mvtnorm::dmvnorm(rep(1.96, 2)), mvnpdf(x =
## matrix(rep(1.96, : less accurate nanosecond times to avoid potential integer
## overflows
mb
## Unit: microseconds
##                                           expr    min     lq     mean median
##                 mvtnorm::dmvnorm(rep(1.96, 2)) 20.254 21.402 23.26033 22.058
##  mvnpdf(x = matrix(rep(1.96, 2)), Log = FALSE) 18.573 19.680 23.18177 20.213
##      uq      max neval cld
##  23.206   98.933  1000   a
##  21.361 1767.346  1000   a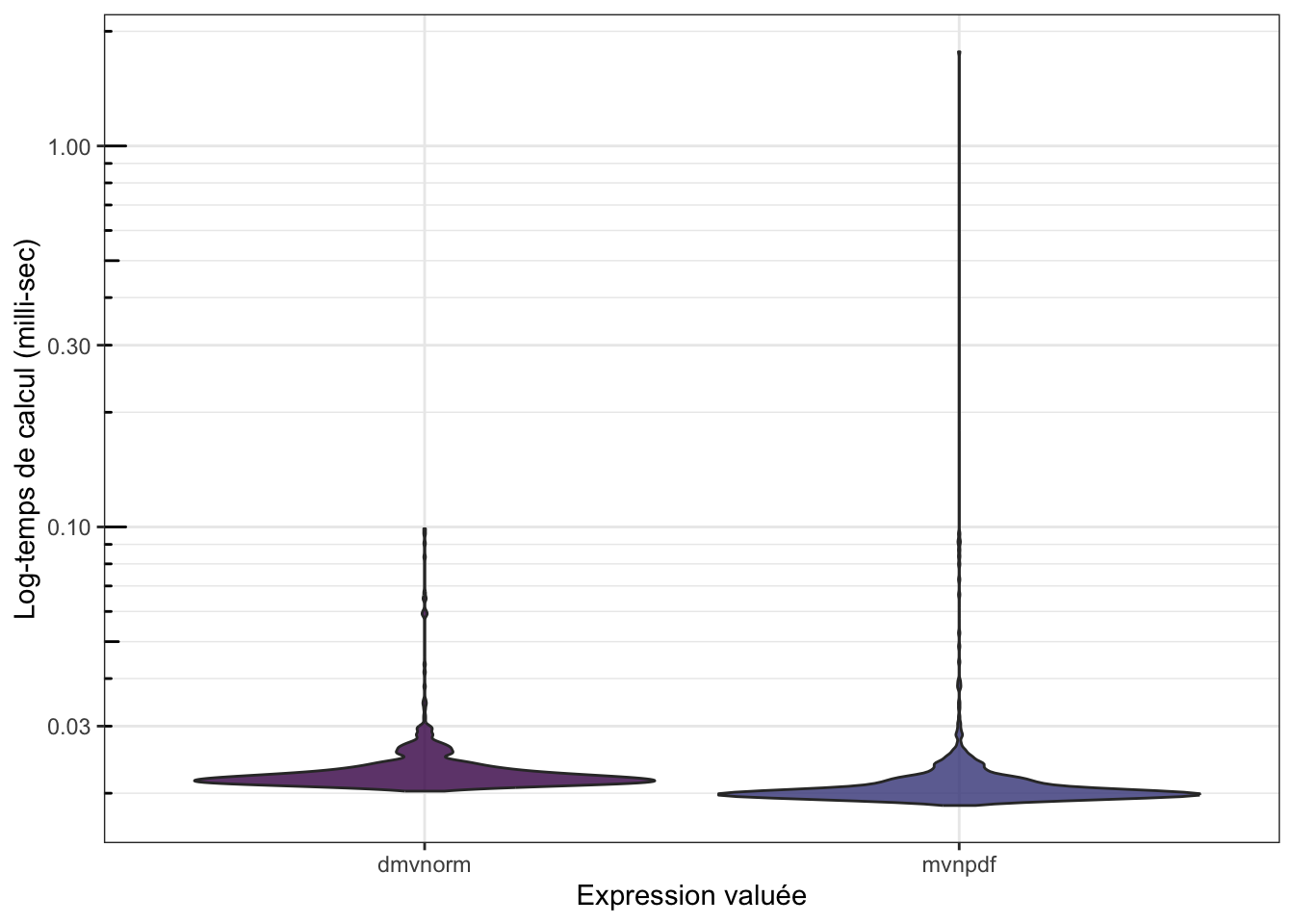

Les deux fonctions mvnpdf() et dmnvorm() étant capables de prendre en entrée une matrice, on peut également comparer leurs comportements dans ce cas :

n <- 100
mb <- microbenchmark(mvtnorm::dmvnorm(matrix(1.96, nrow = n, ncol = 2)),
                     mvnpdf(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
                     times=100L)
mb
## Unit: microseconds
##                                                       expr     min       lq
##         mvtnorm::dmvnorm(matrix(1.96, nrow = n, ncol = 2))  23.698  24.9280
##  mvnpdf(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE) 267.935 274.9665
##       mean   median      uq     max neval cld
##   31.32277  26.4040  30.176 149.076   100  a 
##  285.65848 278.2875 284.376 458.339   100   b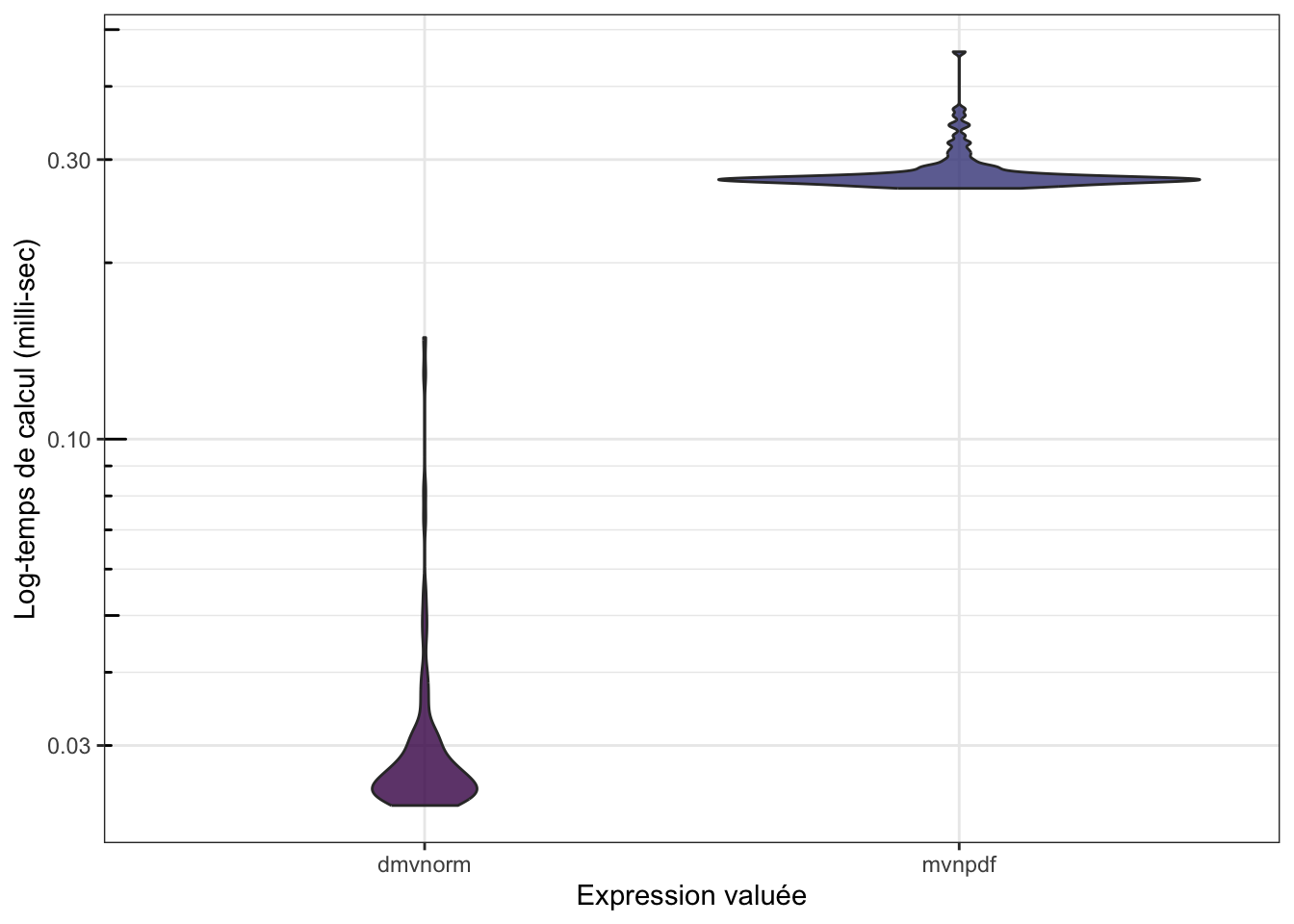

Il s’est passé un quelque chose… Et on va diagnostiquer ce problème dans le prochain chapitre.