Chapitre 3 Mesurer et comparer des temps d’exécution

La première étape avant d’optimiser un code est de pouvoir mesurer son temps d’exécution, afin de pouvoir comparer les temps d’exécution entre différente implémentations.

3.1 Mesurer des temps d’exécution avec system.time()

Pour mesure le temps d’exécution d’une commande R, on peut utiliser la fonction system.time() comme ceci :

system.time(mvnpdf(x=matrix(rep(1.96, 2), nrow=2, ncol=1), Log=FALSE))

##    user  system elapsed 
##   0.001   0.000   0.001

Le problème qui apparaît sur cet exemple est que l’exécution est tellement rapide que system.time() affiche 0 (ou une valeur très proche). De plus, on voit qu’il y a une certaine variabilité quand on relance plusieurs fois la commande.

Ainsi si on souhaite comparer notre code avec la fonction mvtnorm::dmvnorm(), on ne peut pas utiliser system.time() :

system.time(mvtnorm::dmvnorm(rep(1.96, 2)))

##    user  system elapsed 
##   0.004   0.000   0.004

On pourrait se dire qu’il faut augmenter la complexité de notre calcul, mais il y a mieux : utiliser le package microbenchmark !

3.2 Comparer des temps d’exécution avec microbenchmark()

Comme son nom l’indique, ce package permet justement de comparer des temps d’exécution même quand ceux-ci sont très faibles. De plus, la fonction microbenchmark() va répéter un certain nombre de fois l’exécution des commandes et donc va stabiliser le résultat.

library(microbenchmark)
mb <- microbenchmark(mvtnorm::dmvnorm(rep(1.96, 2)),
                     mvnpdf(x=matrix(rep(1.96,2)), Log=FALSE),
                     times=1000L)
mb

## Unit: microseconds
##                                           expr    min      lq     mean
##                 mvtnorm::dmvnorm(rep(1.96, 2)) 41.899 50.3690 65.20473
##  mvnpdf(x = matrix(rep(1.96, 2)), Log = FALSE) 33.479 40.4305 50.17212
##   median      uq      max neval
##  58.6825 67.7505 1822.501  1000
##  46.2140 53.9490  207.524  1000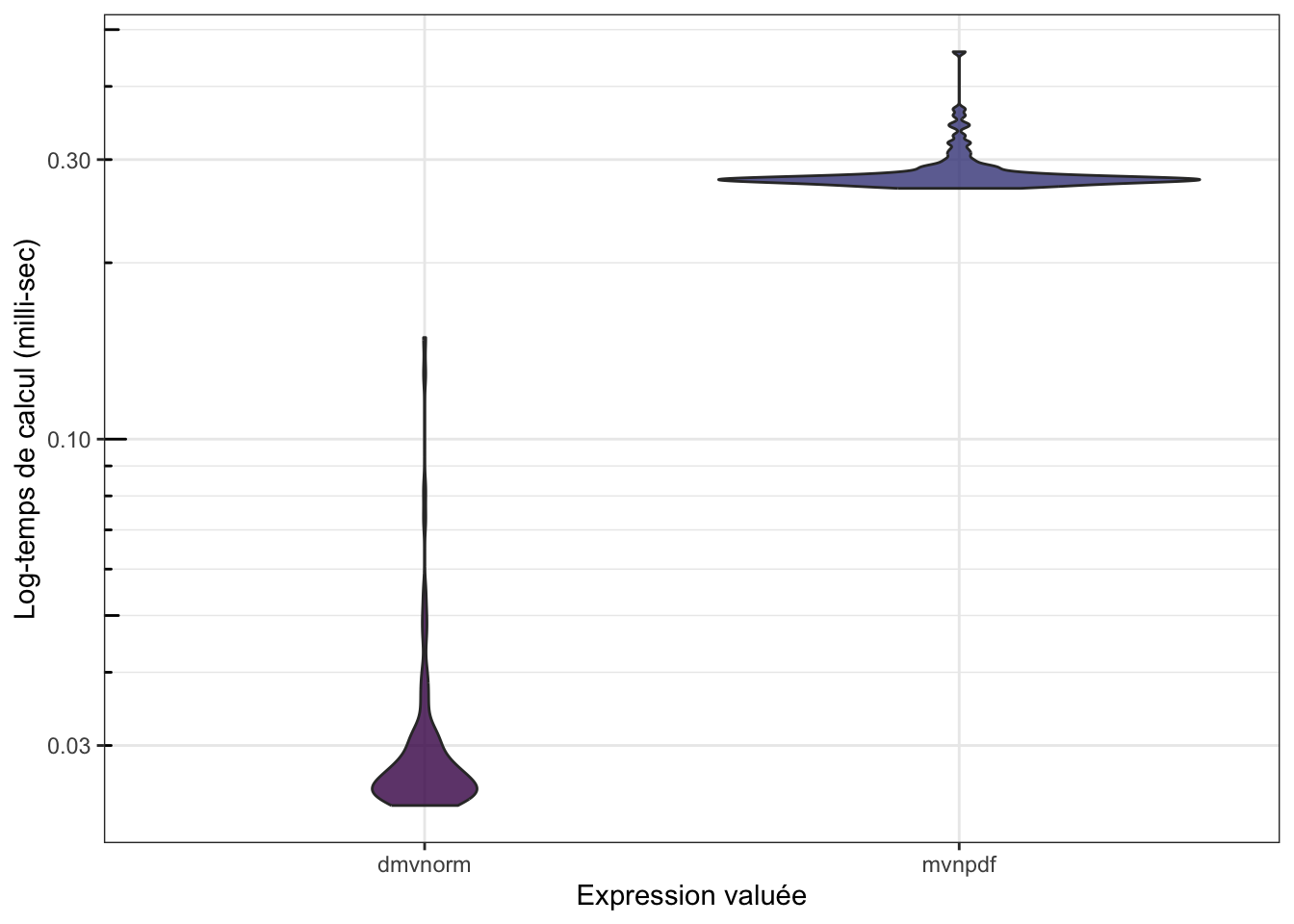

Les deux fonctions mvnpdf() et dmnvorm() étant capables de prendre en entrée une matrice, on peut également comparer leurs comportements dans ce cas :

n <- 100
mb <- microbenchmark(mvtnorm::dmvnorm(matrix(1.96, nrow = n, ncol = 2)),
                     mvnpdf(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
                     times=100L)
mb

## Unit: microseconds
##                                                       expr     min
##         mvtnorm::dmvnorm(matrix(1.96, nrow = n, ncol = 2))  62.328
##  mvnpdf(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE) 456.611
##        lq      mean  median       uq      max neval
##   71.5295  88.33074  77.482 101.4010  193.868   100
##  516.9945 593.73818 554.145 697.3815 1014.220   100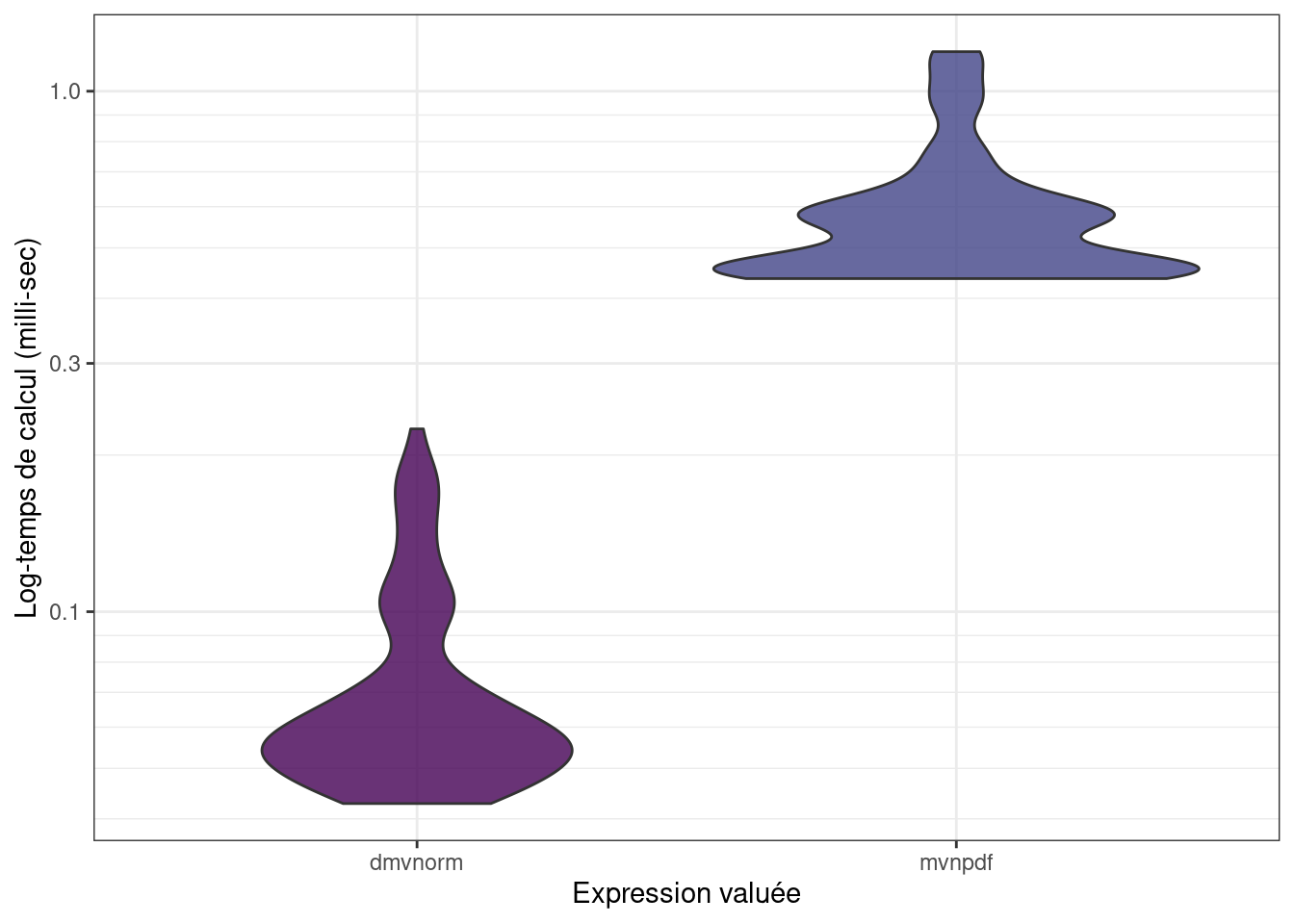

Il s’est passé un quelque chose… Et on va diagnostiquer ce problème dans la suite.