Skip to main content

Formation avancée: Outils de développement et de performance

Chapitre 5 Rcpp ou comment intégrer facilement du code C++dans un package R

Rcpp (R-C-Plus-Plus) est un package qui facilite l’interface entre C++ et R. R est un langage interprété, ce qui facilite un certain nombre de choses (notamment nous donne accès à la console dans laquelle on peut évaluer du code à la volée). Néanmoins, cette facilité d’utilisation se compense entre autre par des temps de calcul supérieurs à ceux de langages de plus bas niveau, tels que C, Fortran et C++ (mais qui nécessitent eux une compilation).

On dirigera le lecteur curieux vers le livre en ligne Rcpp for everyone de Masaki E. Tsuda, qui constitue une ressource très complète pour comprendre l’utilisation de Rcpp en plus de l’introduction que l’on peut trouver dans le livre Advanced R d’Hadley Wickham.

5.1 Première fonction en Rcpp

A vous de jouer !

  1. Afin de rendre votre package prêt pour l’utilisation avec Rcpp, commencez par executer la commande suivante :
devtools::use_rcpp()

  1. Constatez les changements apportés

  2. il faut également ajouter les 2 commentaires roxygen suivants dans la page d’aide du package dans son ensemble :

#' @useDynLib mypkgr
#' @importFrom Rcpp sourceCpp, .registration = TRUE
NULL

Nous allons maintenant créer une première fonction en Rcpp permettant d’inverser une matrice. Pour cela, nous allons nous appuyer sur la library C++ Armadillo. Il s’agit d’une library d’algèbre linéaire moderne et simple, hautement optimisée, et interfacée avec R via le package RcppArmadillo.

C++ n’est pas un langage très différent de R. Les principales différences qui nous concernent :

  • C++est très efficaces pour le boucles for (y compris les boucles for emboîtées). Attention : il y a souvent un sens qui est plus rapide que l’autre (ceci est dû à la manière dont C++ attribue et parcours la mémoire).

  • Chaque commande doit se terminer par un point virgule ‘;’

  • C++est un langage typé : il faut déclarer le type de chaque variable avant de pouvoir l’utiliser.

A vous de jouer !

  1. Créez un nouveau fichier C++ depuis RStudio (via le menu File > New File > C++ File), et enregistrez le dans le dossier src. Prenez le temps de le lire et essayez de comprendre chaque ligne.

  2. Compilez et chargez votre package (via le bouton “Install and Restart”) et essayez d’utiliser la fonction timesTwo() depuis la console.

  3. Installez le package RcppArmadillo, et n’oubliez pas de faire les ajouts nécessaires dans DESCRIPTION (cf. usethis::use_rcpp_armadillo())

  4. À l’aide de l’[introduction à Rcpp]](http://adv-r.had.co.nz/Rcpp.html#rcpp-intro) de Hadley Wickham dans son livre Advanced R, ainsi que de la documentation du package RcppArmadillo de celle de la library C++ Armadillo, tentez d’écrire une courte fonction invC en C++ calculant l’inverse d’une matrice.

  5. Lorsque vous avez réussi à compiler votre fonction invC et qu’elle est accessible depuis créer une fonction mvnpdf_invC() à partir de l’implémentation de mvnpdfsmart en remplaçant uniquement les calculs d’inverse matriciel par un appel à invC.

  6. Evaluer le gain en performance de cette nouvelle implémentation mvnpdf_invC.

n <- 1000
mb <- microbenchmark(mvtnorm::dmvnorm(matrix(1.96, nrow = n, ncol = 2)),
                     mvnpdf(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
                     mvnpdfsmart(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
                     mvnpdfoptim(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
                     mvnpdf_invC(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
                     times=100L)
mb
## Unit: microseconds
##                                                            expr      min
##              mvtnorm::dmvnorm(matrix(1.96, nrow = n, ncol = 2))   44.977
##       mvnpdf(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE) 3315.752
##  mvnpdfsmart(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE) 2317.976
##  mvnpdfoptim(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE) 1749.224
##  mvnpdf_invC(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE) 2318.017
##         lq       mean    median        uq       max neval  cld
##    67.3425   80.78763   79.8065   94.7715   136.284   100 a   
##  3452.2000 3814.73348 3520.5470 3737.4780 11503.985   100  b  
##  2375.6835 2546.84825 2398.5820 2443.0670  6170.336   100   c 
##  1812.3845 1903.67961 1851.9495 1905.3520  5399.454   100    d
##  2361.3335 2510.35825 2390.5665 2434.7645  6297.723   100   c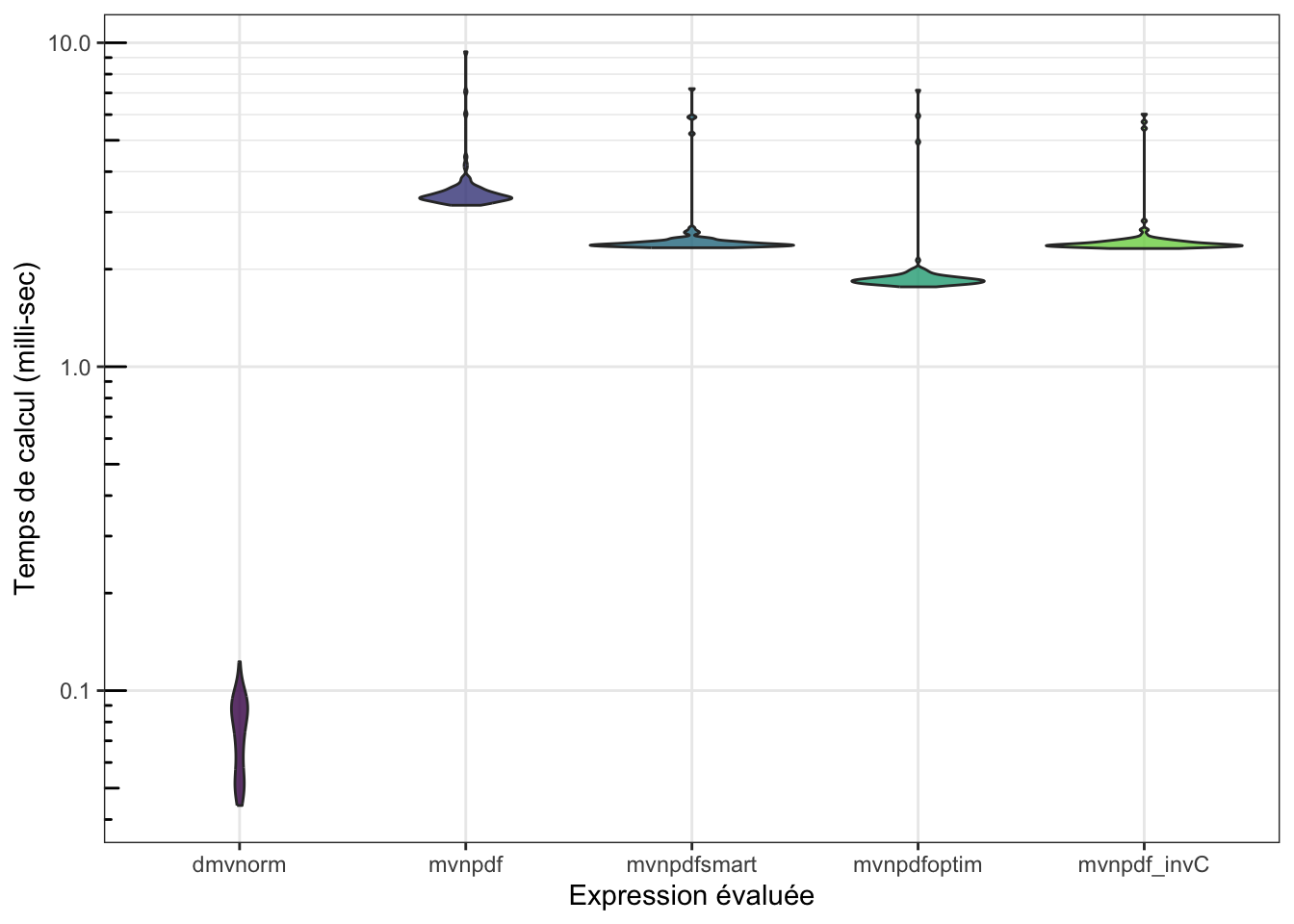
profvis::profvis(mvnpdfoptim(x=matrix(1.96, 
    nrow = 2, ncol = 1000), Log=FALSE))
profvis::profvis(mvnpdfoptim(x=matrix(1.96, 
    nrow = 100, ncol = 1000), Log=FALSE))

5.2 Optimisation grâce à C++

En règle générale, on ne gagne pas beaucoup en temps de calcul en remplaçant une fonction R optimisée par une fonction en C++. En effet, la plupart des fonctions de base de R s’appuie en réalité déjà sur des routines C ou Fortran bien optimisée. Le gain se limite alors simplement à la suppression des vérifications des arguments et de la gestion des différents types.

A vous de jouer !

  1. À partir de mvnpdfsmart, proposez une implémentation completement en C++ du calcul de densité de la loi Normale multivariée mvnpdfC().

  2. Evaluer le gain en performance de cette nouvelle implémentation mvnpdfC

Vous pouvez télécharger notre proposition de mvnpdfC.cpp ici.

n <- 1000
mb <- microbenchmark(mvtnorm::dmvnorm(matrix(1.96, nrow = n, ncol = 2)),
                     mvnpdf(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
                     mvnpdfsmart(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
                     mvnpdfoptim(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
                     mvnpdf_invC(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
                     mvnpdfC(x=matrix(1.96, nrow = 2, ncol = n), mean = rep(0, 2), varcovM = diag(2), Log=FALSE),
                     times=100L)
mb
## Unit: microseconds
##                                                                                                  expr
##                                                    mvtnorm::dmvnorm(matrix(1.96, nrow = n, ncol = 2))
##                                             mvnpdf(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE)
##                                        mvnpdfsmart(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE)
##                                        mvnpdfoptim(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE)
##                                        mvnpdf_invC(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE)
##  mvnpdfC(x = matrix(1.96, nrow = 2, ncol = n), mean = rep(0, 2),      varcovM = diag(2), Log = FALSE)
##       min        lq       mean    median        uq      max neval  cld
##    44.608   57.5025   78.25465   80.1140   93.7260  123.287   100 a   
##  3340.475 3477.2920 3745.40330 3543.2405 3661.5665 8599.627   100  b  
##  2322.199 2375.3350 2482.04570 2407.9505 2439.4385 6698.129   100   c 
##  1745.903 1823.2085 2027.96824 1863.0400 1915.9505 6711.659   100    d
##  2317.074 2366.0895 2516.76532 2402.1285 2439.4385 6947.655   100   c 
##    35.506   43.5625   55.14500   47.0475   53.5255  713.441   100 a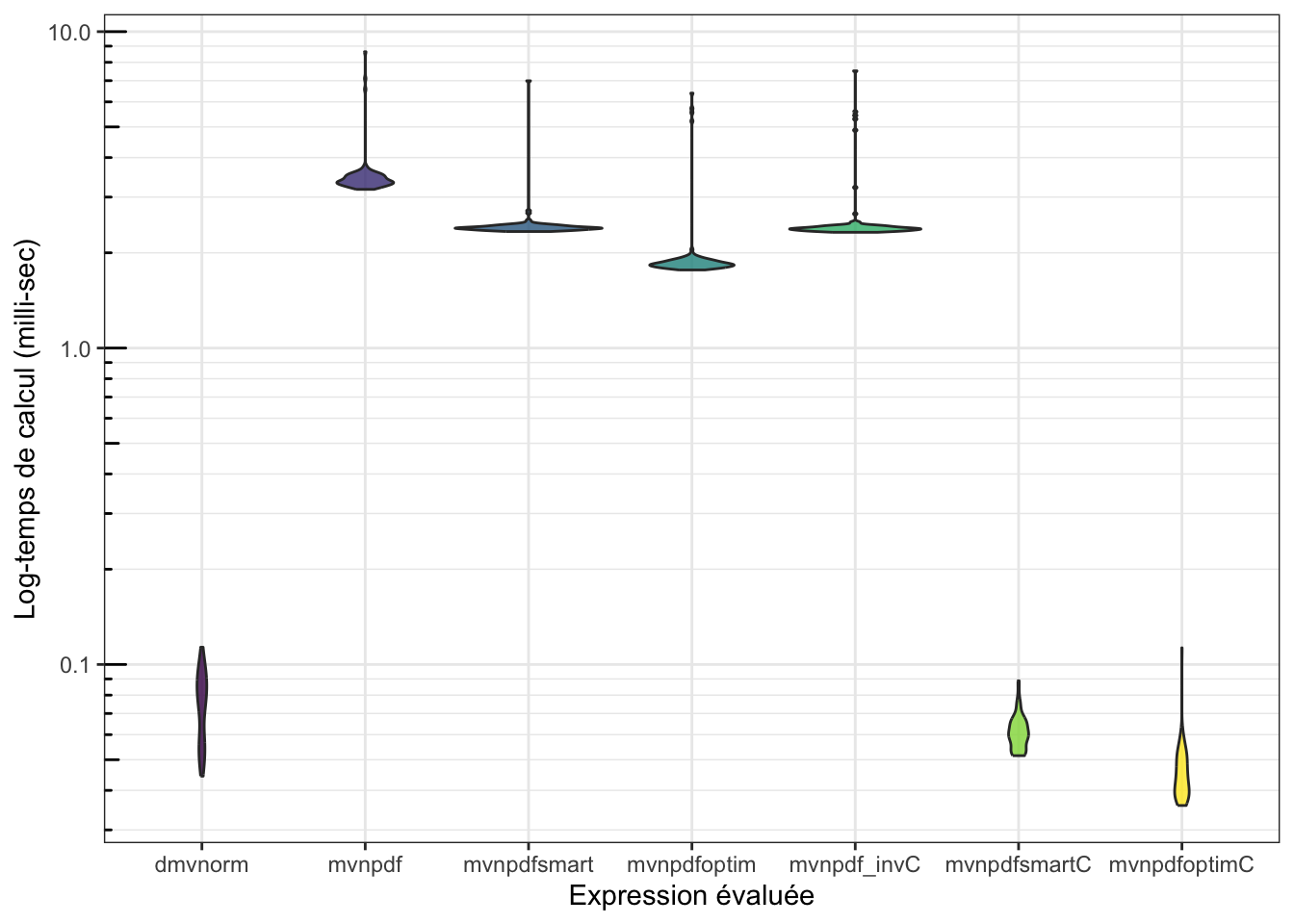

À noter que vous pouvez utiliser des fonctions Rcpp en dehors de l’architecture d’un package grâce à la fonction Rcpp::sourceCpp(). Mais comme nous avons qu’il est préférable de gérer tous ces code sous la forme de package, il est peu probable que vous en ayez besoin !

5.3 Annexe 5.1 : l’optimisation prématurée n’est pas une bonne idée

Chambers, Software for Data Analysis: Programming with R, Springer, 2008 :

Including additional C code is a serious step, with some added dangers and often a substantial amount of programming and debugging required. You should have a good reason.